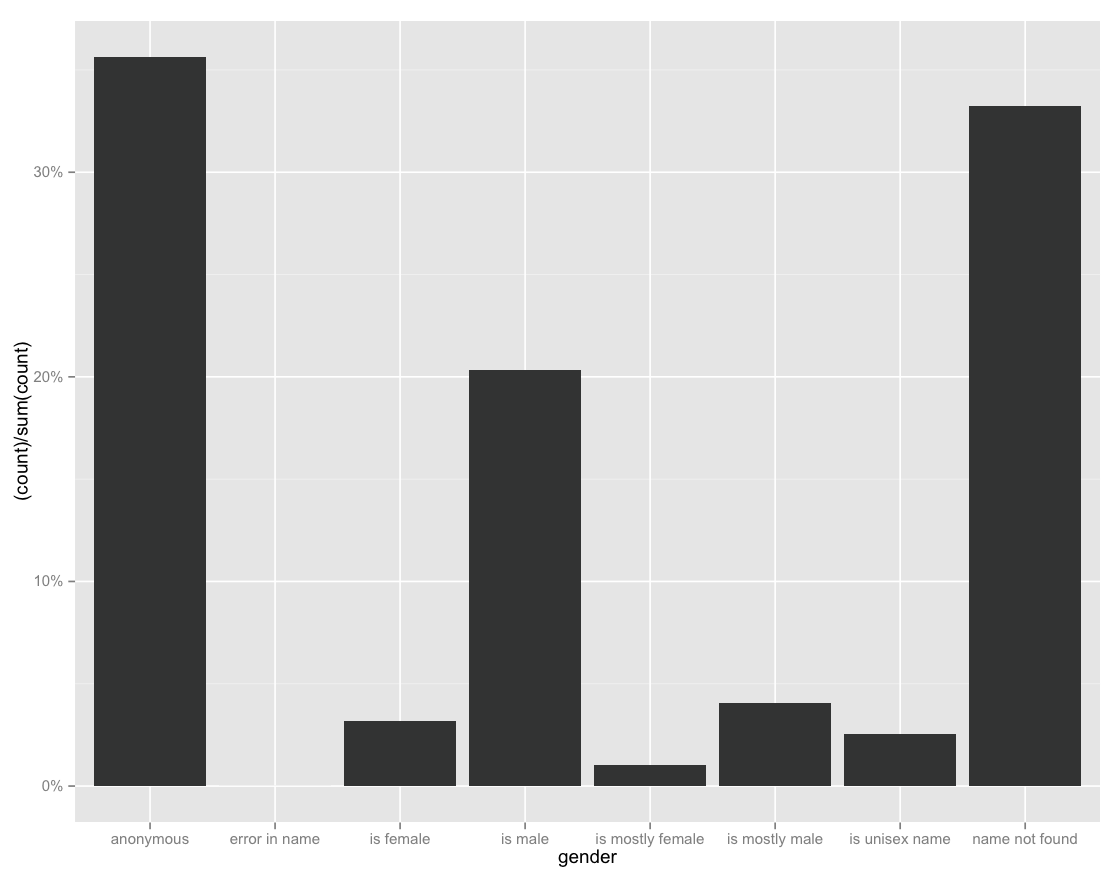
My previous post was an introduction to the motivations and benefits of a property-based testing approach.

I also mentioned the John Hughes talk, which is great.

But there’s a catch.

Until now, we’ve been considering property-based testing in a functional way, where properties for functions depend only on the function input, assuming no state between function invocations.

But that’s not always the case, sometimes our function inserts data into some database, sends an email, or sends a message to the car anti-lock braking system.

The examples John mentions in his talk are not straightforward to solve without Erlang’s QuickCheck, since they’re verifying state machines behavior.

Since I’m a Clojurist, I was a little confused about why I couldn’t find a way to do that state machine magic using test.check, so bugging Reid and not reading the fine manual was the evident answer.

Thing is, test.check has this strategy of composing generators, particularly using bind you can generate a value based on a previously generated value by another generator.

For instance, this example shows how to generate a vector and then select an element from it:

1
2
3
4
5
6
7

(def keyword-vector (gen/such-that not-empty (gen/vector gen/keyword)))
(def vec-and-elem
  (gen/bind keyword-vector
            (fn [v] (gen/tuple (gen/elements v) (gen/return v)))))

(gen/sample vec-and-elem 4)
;; => ([:va [:va :b4]] [:Zu1 [:w :Zu1]] [:2 [:2]] [:27X [:27X :KW]])

But it doesn’t have a declarative or simple way to model expected system state.

What is state?

First thing we should think about is, when we do have state? Opposed to a situation when we’re testing a referentially transparent function.

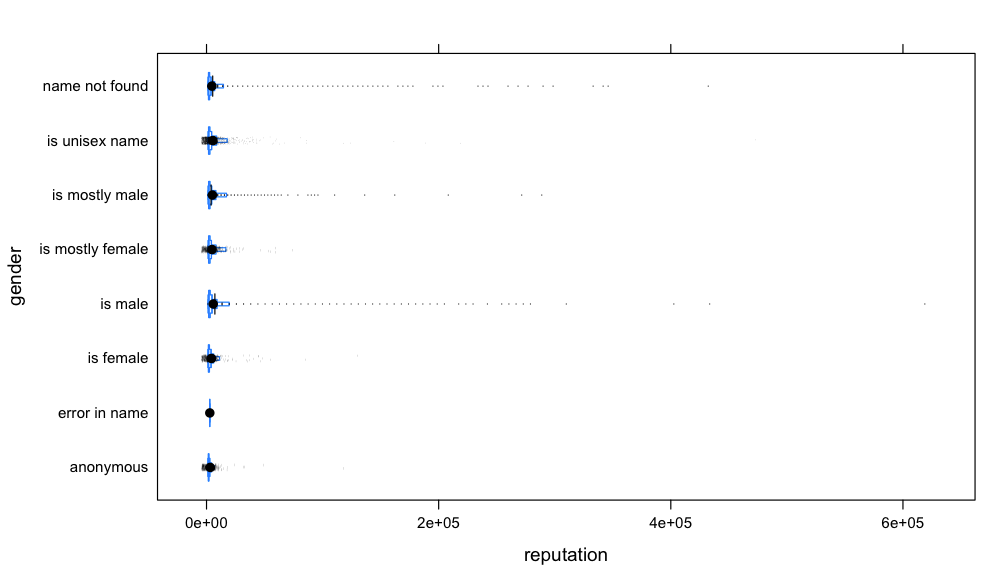
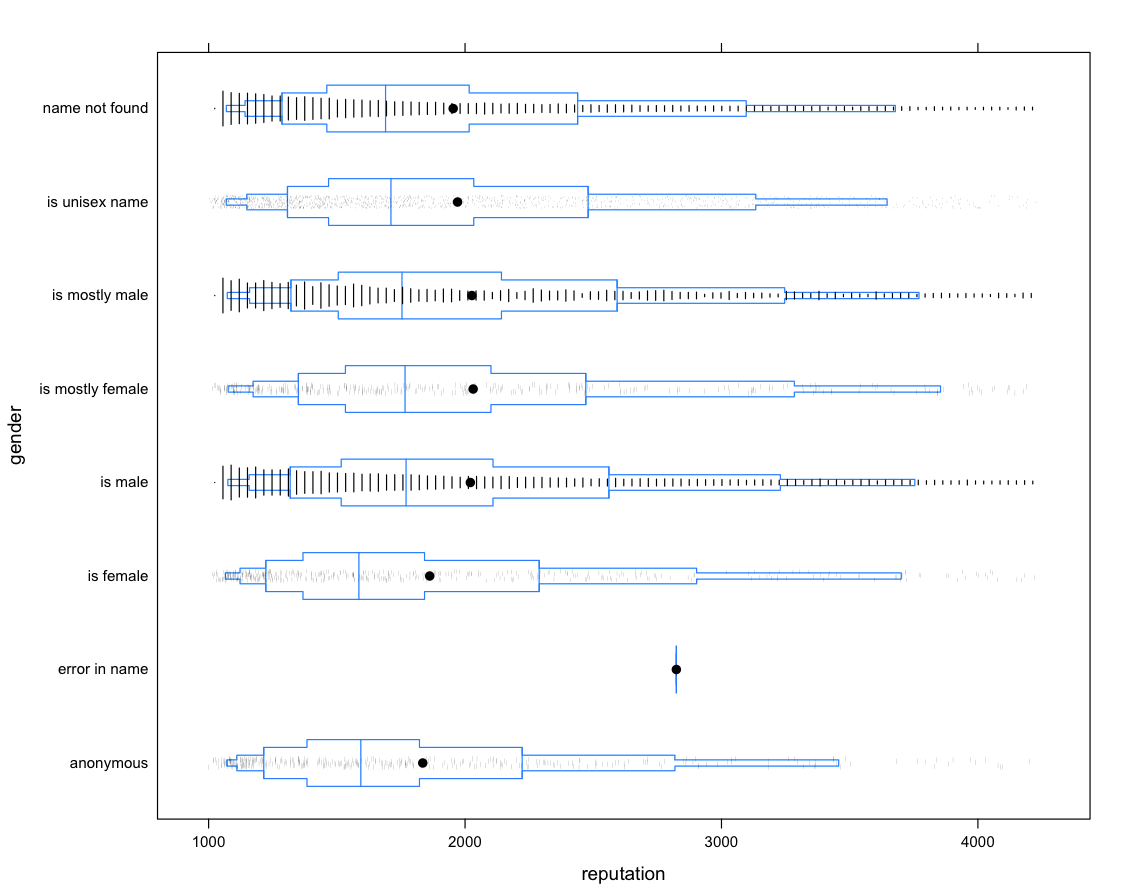
The function sort from the previous post is referentially transparent, since for the same input vector, always return the same sorted output.

But what happens when we have a situation like the one described in the talk about this circular buffer?

If you want to test the behavior of the put and remove API calls, it depends on the state of the system, meaning what elements you already have on your buffer.

The properties put must comply with, depend on the system state.

So you have this slide from John’s presentation:

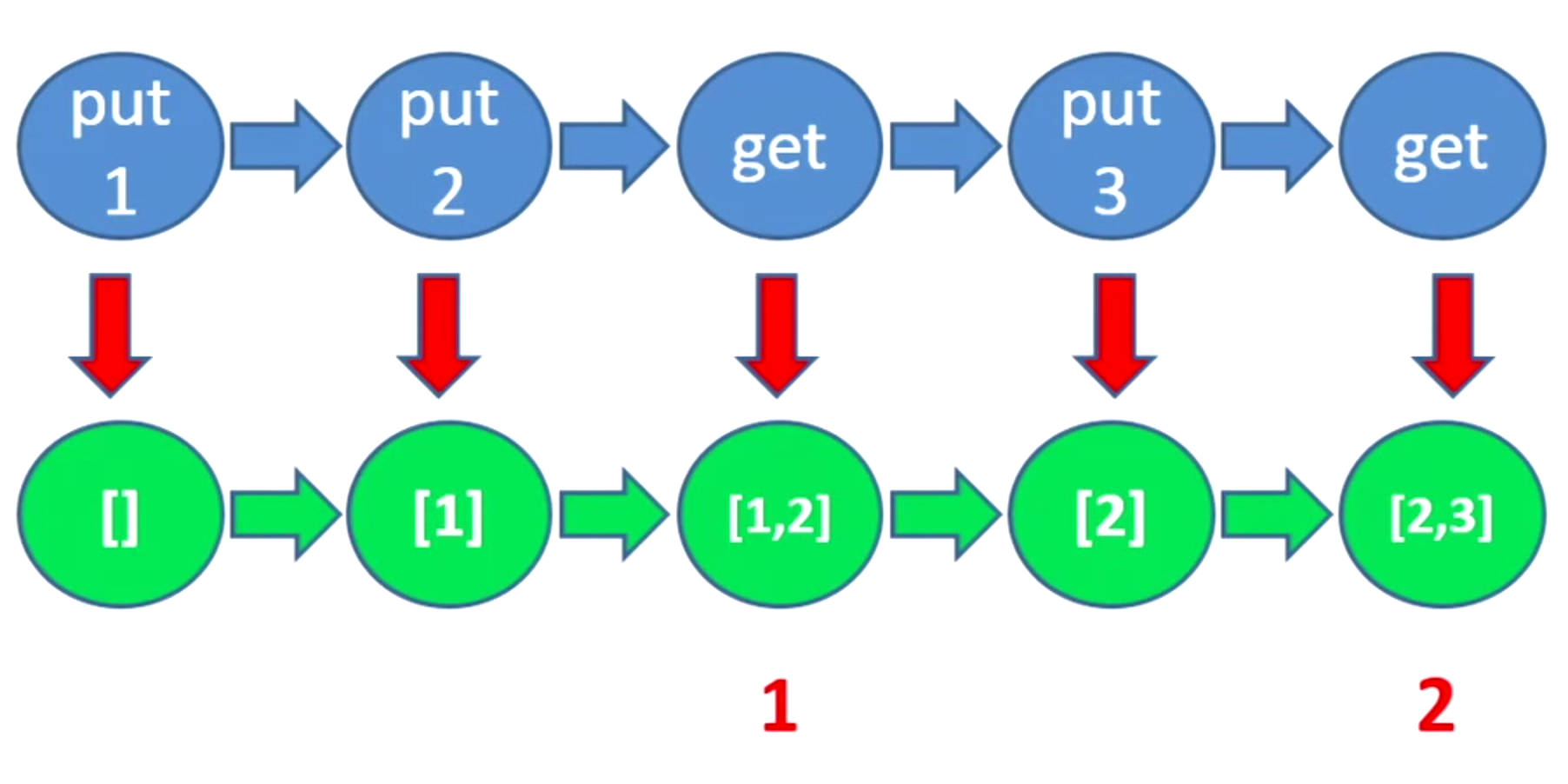
With the strategy proposed by QuickCheck to model this testing problem:

• API under test is seen as a sequence of commands.
• Model the state of the system you expect after each command execution.
• Execute the commands and validate the system state is what you expect it to be.

So we need to generate a sequence of commands and validate system state, instead of generating input for a single function.

This situation is more common than you may think, even if you’re doing functional programming state is everywhere, you have state on your databases and you also have state on your UI.

You would never think about deleting an email, and after than sending the email, that’s an invalid generated sequence of commands(relative to the “email composing state”).

This last example is exactly the one described by Ashton Kemerling from Pivotal, they’re using test.check to randomly generate test scenarios for the UI. And because test.check doesn’t have the finite state machine modeling thing, they ended up generating impossible or invalid action sequences, and having to discard them as NO-OPs when run.

FSM Behavior

The problem with Ashton’s approach for my situation, was that I had this possibly long sequence of commands or transactions, where each transaction modifies the state of the system, so the last one probable makes no sense at all without some of the in-the-middle ocurring transactions.

The problem is not only discarding invalid sequences, but how to generate something valid at all.

Say you have 3 possible actions:

• add [id, name]
• edit [id, name]
• delete [id]

If the command sequence you generate is:

1
2
3

[{:type :add :name "John" :id 1}
 {:type :add :name "Ted" :id 84}
 {:type :delete :id 1}]

The delete action depends on two things:

1. Someone to be already added (as in the circular buffer described above).
2. Selecting a valid id for deletion from the ones already added.

It looks like something you would do using bind, but there’s something more, there’s a state that changes when each transaction is applied, and affects each potential command that may be generated afterwards.

Searching around, I found a document titled Verifying Finite State Machine Behavior Using QuickCheck Eqc_fsm by Ida Lindgren and Robin Malmros, it’s an evaluation from Uppsala Universitet to understand whether QuickCheck is suitable for testing mobile telephone communications with base transceiver stations.

Besides the evaluation itself which is worth reading, there’s a chapter on Finite State Machines I used as guide to implement something similar with test.check.

The Command protocol

There’s a nice diagram in the paper representing the Erlang’s finite state machine flow

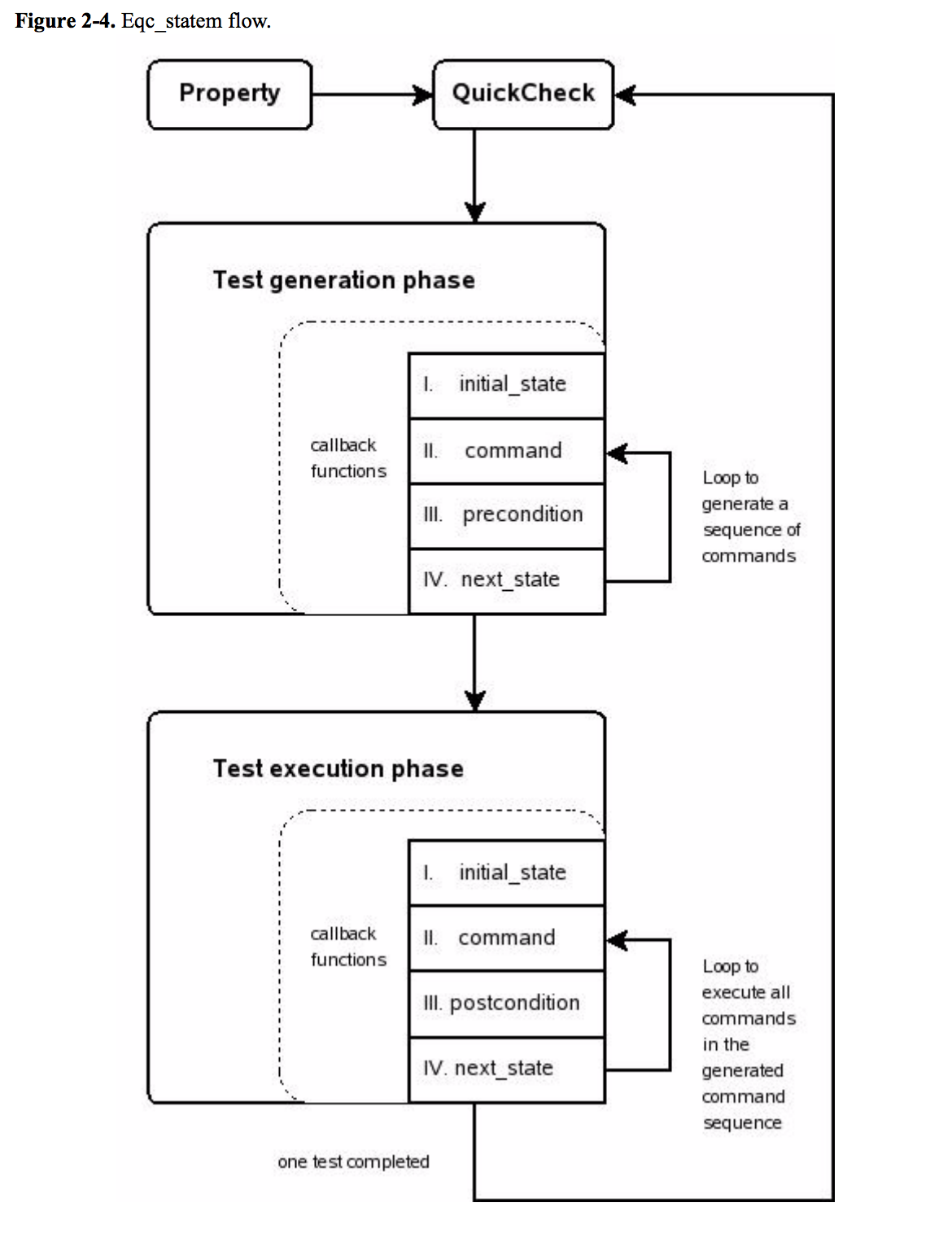
We observe a few things:

• You have a set of possible commands to generate.
• Each command has a precondition to check validity against current state.
• Each command affects state in some way, generating a new-state.

Translating that ideas into Clojure we can model a command protocol

1
2
3
4

(defprotocol Command
  (precondition [this state] "Returns true if command can be applied in current system state")
  (exec [this state cmd] "Applies generated command to the specified system state, returns new state")
  (generate [this state] "Generates command given the current system state, returns command generator"))

So far, we’ve assumed nothing about:

• How state is going to be modeled.
• What structure each generated command has.

Since we’re using test.check we need a particular protocol function generate returning the command generator.

A Command generator

Having a protocol, lets define our add, edit and delete transactions.

Questions to answer are:

1. What will our model of the world look like?
2. What’s the initial and expected states after applying each transaction?

Our expected state will be something like this:

1
2
3

{:people [{:name "John" :id 1}
          {:name "Ted" :id 84}
          {:name "Tess" :id 22}]}

So our add transaction will be:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

(def add-cmd
  (reify
    Command
    (precondition [_ state]
      (vector? (:people state)))

    (exec [_ state cmd]
      (update-in state [:people] (fn [people]
                                   (conj people
                                         (dissoc cmd :type)))))
    (generate [_ state]
      (gen/fmap (partial zipmap [:type :name :id])
                (gen/tuple (gen/return :add)
                           (gen/not-empty gen/string-alphanumeric)
                           gen/int))))))

The highlights:

• Our only precondition is to have a vector to conj the transaction into.
• The generate function returns a standard test.check generator for the command.
• The exec function applies the generated command to the current system state and returns a new state.

Now, what’s interesting is the delete transaction:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

(def delete-cmd
  (reify
    Command
    (precondition [_ state]
      (seq (:people state)))

    (exec [_ state cmd]
      (update-in state [:people] (fn [people]
                                   (vec (filter #(not= (:id %)
                                                       (:id cmd))
                                                people)))))

    (generate [_ state]
      (gen/fmap (partial zipmap [:type :id])
                (gen/tuple (gen/return :delete)
                           (gen/elements (mapv :id (:people state))))))))

Note the differences:

• delete can only be executed if the people list actually has someone inside
• The generator selects to delete an id from the people in the current state (using gen/elements selector)
• Applying the command implies removing the selected person from the next state.

Valid sequence generator

So how do we generate a sequence of commands giving a command list?

This is a recursive approach, that receives the available commands and the sequence size to generate:

1
2
3
4
5
6
7
8
9
10
11
12
13

(defn command-seq
  [state commands size]
  (gen/bind (gen/one-of (->> (map second commands)
                             (filter #(precondition % state))
                             (map #(generate % state))))
            (fn [cmd]
              (if (zero? size)
                (gen/return [cmd])
                (gen/fmap
                 (partial concat [cmd])
                 (command-seq (exec (get commands (:type cmd)) state cmd)
                              commands
                              (dec size)))))))

The important parts being:

• Selects only one valid command to generate with one-of after filtering preconditions.
• If command sequence size is 0 just finish, otherwise recursively concat the rest of the sequence.
• The new state is updated in the step (exec (get commands (:type cmd)) state cmd), where we need to retrieve the original command object.

If you would like to generate random sequence sizes, just bind it with gen/choose.

1
2
3
4
5
6

(gen/bind (gen/choose 0 10)
          (fn [num-elements]
            (command-seq {:people []}
                         {:add-cmd add-cmd
                          :delete-cmd delete-cmd}
                         num-elements)))

Note the initial state is set to {:people []} for the add command precondition to succeed.

If we generate 3 samples now, it looks good, but there’s still a problem….

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

(({:id 0, :name "C", :type :add-cmd}
  {:id 0, :name "2", :type :add-cmd}
  {:id 0, :name "xi", :type :add-cmd}
  {:id 0, :name "p", :type :add-cmd}
  {:id 0, :type :delete-cmd}
  {:id 0, :name "3Q", :type :add-cmd}
  {:id 0, :name "9", :type :add-cmd}
  {:id 0, :type :delete-cmd})
 ({:id -1, :name "H", :type :add-cmd}
  {:id -1, :type :delete-cmd}
  {:id 1, :name "q", :type :add-cmd}
  {:id 0, :name "F", :type :add-cmd}
  {:id 1, :type :delete-cmd})
 ({:id -1, :name "fY", :type :add-cmd}
  {:id 0, :name "a", :type :add-cmd}
  {:id -1, :type :delete-cmd}
  {:id 2, :name "u", :type :add-cmd}
  {:id 2, :type :delete-cmd}
  {:id 1, :name "7", :type :add-cmd}
  {:id -1, :name "E", :type :add-cmd}
  {:id 1, :type :delete-cmd}
  {:id 0, :type :delete-cmd}
  {:id -1, :type :delete-cmd}))

Each add-cmd is repeating the id, since it’s generating it without checking the current state, let’s change our add transaction generator

1
2
3
4
5
6
7
8

(generate [_ state]
          (gen/fmap (partial zipmap [:type :name :id])
                    (gen/tuple (gen/return :add-cmd)
                               (gen/not-empty gen/string-alphanumeric)
                               (gen/such-that #(-> (mapv :id (:people state))
                                                   (contains? %)
                                                   not)
                                              gen/int))))

Now the id field generator checks that the generated int doesn’t belong to the current ids in the state (we could have returned a uuid or something else, but it wouldn’t make the case for state-dependent generation)

To complete the example we need:

• To apply the commands to the system under test.
• A way to retrieve the system state.
• Comparing the final system state with our final generated expected state.

Which is pretty straightforward, so we’ll talk about shrinking first.

Shrinking the sequence

If you were to found a failing command sequence using the code above, you would quickly realize it doesn’t shrink properly.

Since we’re generating the sequence composing bind, fmap and concat and not using the internal gen/vector or gen/list generators, the generated sequence doesn’t know how to shrink itself.

If you read Reid’s account on writing test.check, there’s a glimpse of the problem we face, shrinking depends on the generated data type. So a generated int knows how to shrink itself, which is different on how a vector shrinks itself.

If you combine existing generators, you get shrinking for free, but since we’re generating our sequence recursively with concat we’ve lost the vector type shrinking capability.

And there’s a good reason it is so, but let’s first see how shrinking works in test.check.

Rose Trees

test.check complects the data generation step with the shrinking of that data. So when you generate some value, behind the scenes all the alternative shrinked scenarios are also generated.

Let’s sample an int vector generator:

1
2

(gen/sample (gen/not-empty (gen/vector gen/int)) 5)
=> ([0] [1] [-1 1] [1 1 -3] [2 3])

The sample function is hiding from you the alternatives and showing only the actual generated value.

But, if we call the generator using call-gen, we have a completely different structure:

1
2

(gen/call-gen (gen/not-empty (gen/vector gen/int)) (gen/random) 1)
=> [[1] ([[0] ()])]

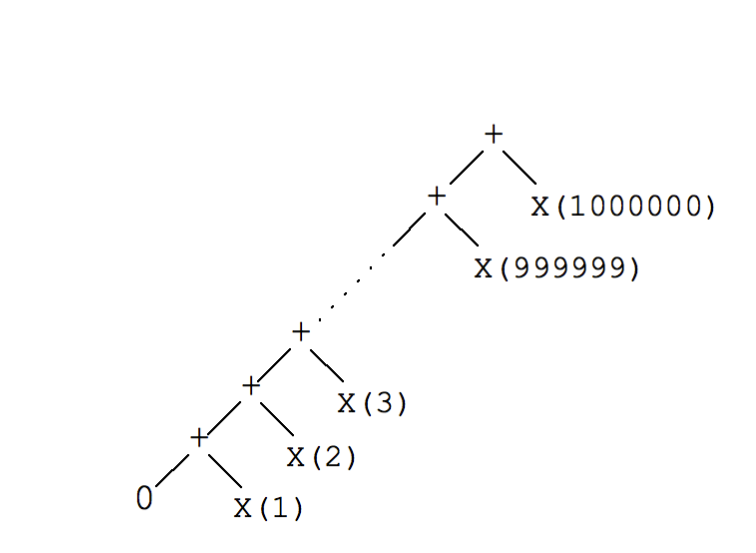
What we have is a rose tree, which is a n-ary tree, where each tree node may have any number of childs.

test.check uses a very simple modeling approach for the tree, in the form of [parent childs].

So this tree

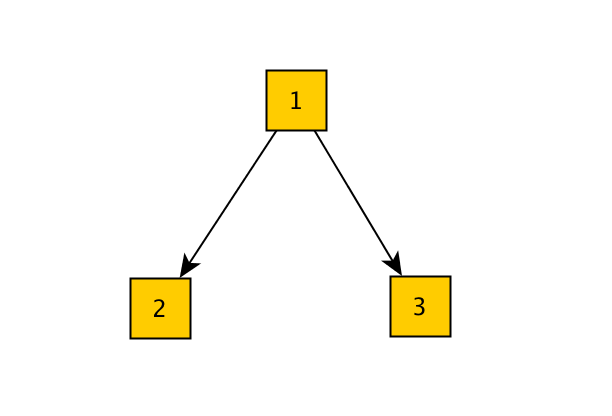
Is represented as

1
2

[1 [[2 []]
    [3 []]]]

Everytime you get a generated value, what you’re looking at is at the root of the tree obtained with rose/root, which is exactly what gen/sample is doing.

1
2
3
4

(require '[clojure.test.check.rose-tree :as rose])

(rose/root (gen/call-gen (gen/not-empty (gen/vector gen/int)) (gen/random) 1))
=> [0]

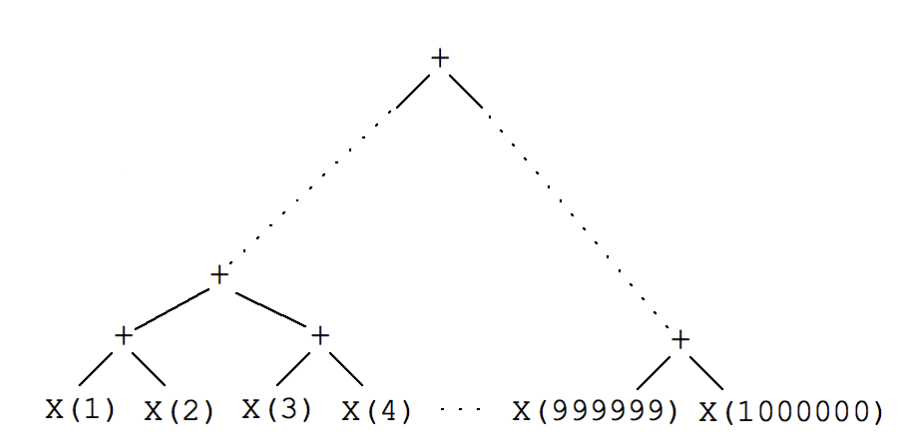
The shrinking tree you would expect for a generated vector is:

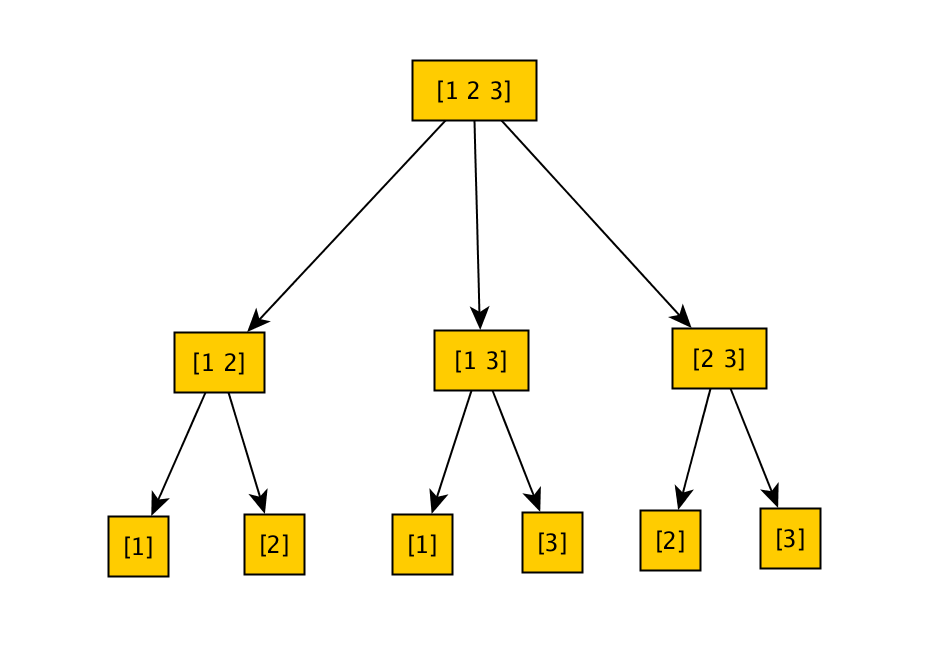
The more deep inside the tree, the more shrunk the value is. So for instance integers shrink up to zero, and vectors randomly remove elements until nothing is left.

If we were to actually look inside the shrunk vector tree, it would also include the shrunked integers, but you get the idea.

Shrinking a valid command sequence

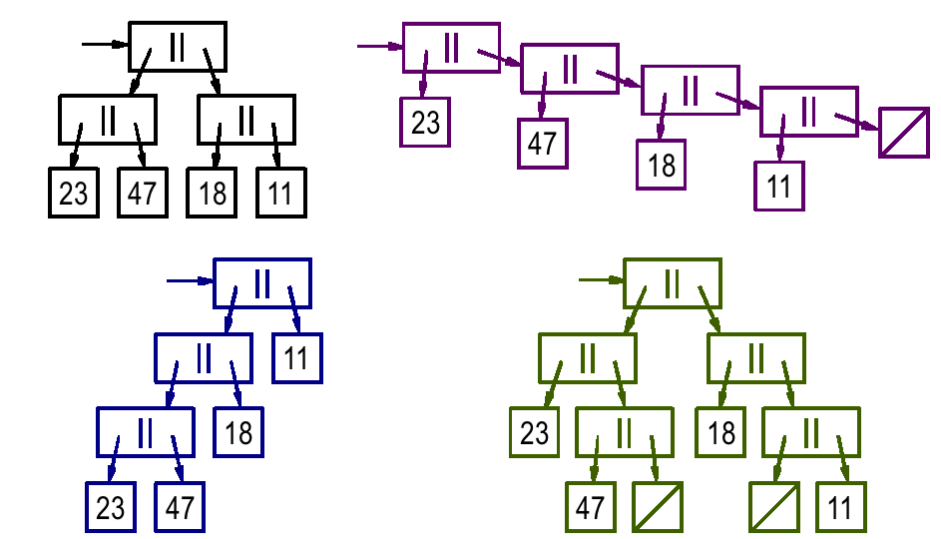
I said before our sequence doesn’t shrink since it’s generated recursively, so this is how our sequence tree looks like so far.

But even if we were using the vector shrinker we would end up with something like this:

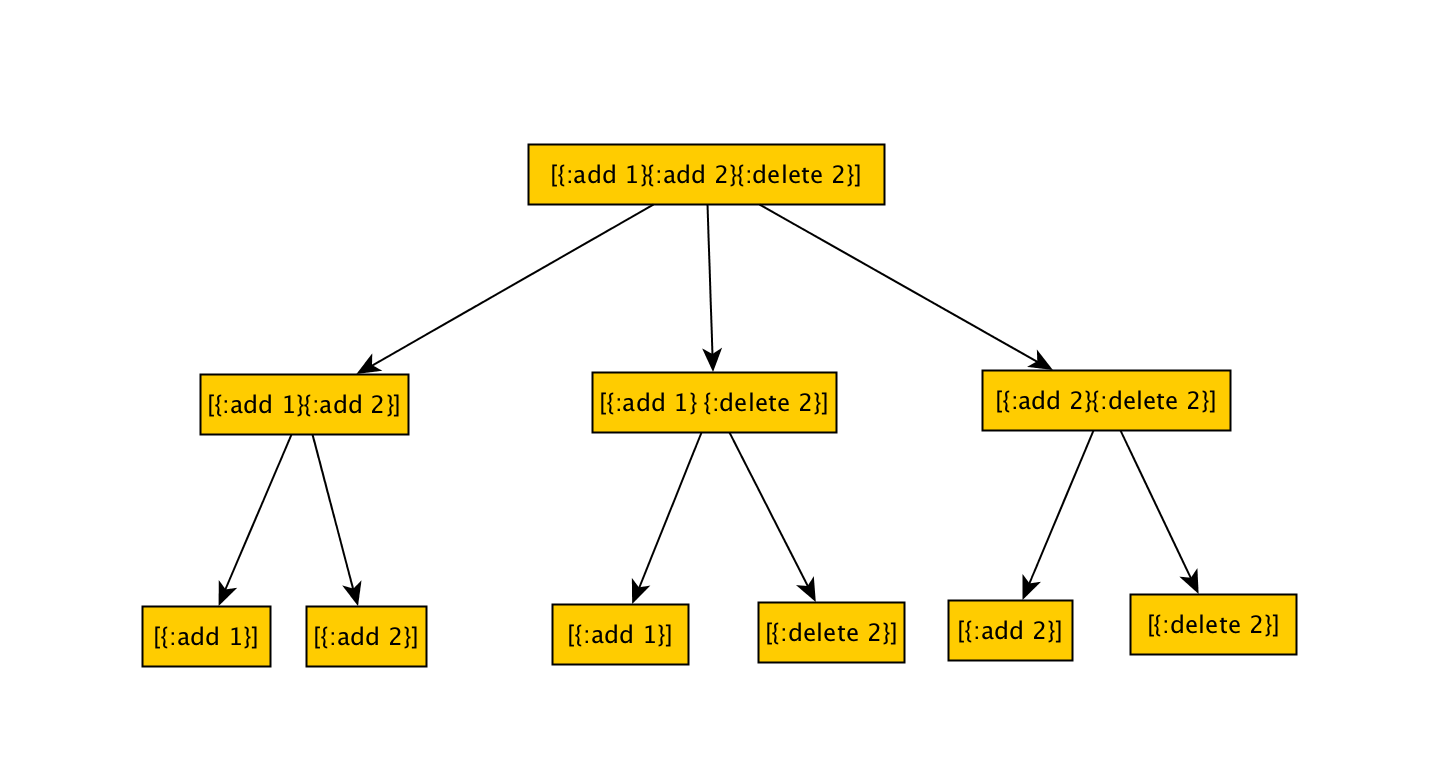
Since the vector shrinker doesn’t really know what a valid command sequence looks like, it will just do a random permutation of commands, ending up with many invalid sequences (like [{:add 1} {:delete 2}]).

We will need a custom shrinker, that shrinks only valid command sequences, with a resulting tree like this one:

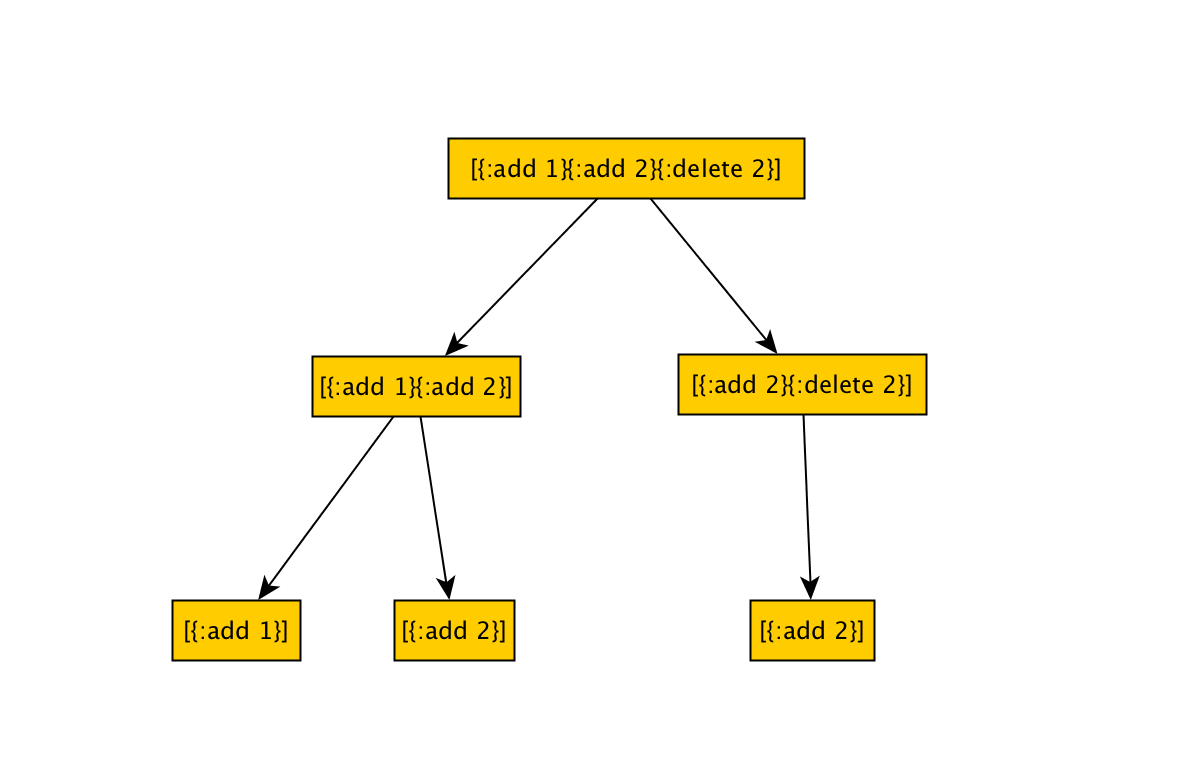
To do that, we will modify our protocol to add a new function postcondition.

1
2
3
4
5

(defprotocol Command
  (precondition [this state] "Returns true if command can be applied in current system state")
  (exec [this state cmd] "Applies generated command to the specified system state, returns new state")
  (generate [this state] "Generates command given the current system state, returns command generator"))
  (postcondition [this state cmd] "Returns true if cmd can be applied on specified state"))

postcondition will be called while shrinking, in order to validate if a shirking sequence is valid for the hipotetical state generated by the previous commands.

Another important function is gen/pure, which allows to return our custom rose tree as generator result.

So this is how our command generator looks like now:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

(defn cmd-seq
  [state commands]
  (gen/bind (gen/choose 0 10)
            (fn [num-elements]
              (gen/bind (cmd-seq-helper state commands num-elements)
                        (fn [cmd-seq]
                          (let [shrinked (shrink-sequence (mapv first cmd-seq)
                                                          (mapv second cmd-seq))]
                            (gen/gen-pure shrinked)))))))


(defn cmd-seq-helper
  [state commands size]
  (gen/bind (gen/one-of (->> (map second commands)
                             (filter #(precondition % state))
                             (map #(generate % state))))
            (fn [cmd]
              (if (zero? size)
                (gen/return [[cmd state]])
                (gen/fmap
                 (partial concat [[cmd state]])
                 (cmd-seq-helper (exec (get commands (:type cmd)) state cmd)
                                 (map second commands)
                                 (dec size)))))))

We see two different things here:

1. Generator also returns the state for that particular command.
2. There’s a call to shrink-sequence that generates the rose tree given the command sequence and intermediate states.

The shrink-sequence function being:

1
2
3
4
5
6
7
8
9

(defn shrink-sequence
  [cmd-seq state-seq]
  (letfn [(shrink-subseq [s]
            (when (seq s)
              [(map #(get cmd-seq %) s)
               (->> (remove-seq s)
                    (filter (partial valid-sequence? state-seq cmd-seq))
                    (mapv shrink-subseq))]))]
    (shrink-subseq (range 0 (count cmd-seq)))))

Highlights:

• Returns a rose tree in the form [parent childs].
• remove-seq generates a sequence of subsequences with only one element removed.
• valid-sequence? uses postcondition to validate the shrinked seq.
• Recursively shrinks the shrunk childs until nothing’s left.

Putting all together

I’ve put together a running sample for you to check out here.

There’s only one property defined: applying all the generated transactions should return true, but it fails when there are two delete commands present.

1
2
3
4
5
6
7
8
9
10
11

(defn apply-tx
  "Apply transactions fails when there are two delete commands"
  [tx-log]
  (->> tx-log
       (filter #(= :delete-cmd (:type %)))
       count
       (> 2)))

(def commands-consistent-apply
  (prop/for-all [tx-log (cmd-seq {:people []} {:add-cmd add-cmd :delete-cmd delete-cmd})]
                (true? (apply-tx tx-log))))

1
2
3
4
5
6
7
8
9
10
11
12
13
14

(tc/quick-check 10 commands-consistent-apply)
=>

{:result false, :seed 1428695347616, :failing-size 7, :num-tests 8,
 :fail [({:id 6, :name "8", :type :add-cmd}
         {:id -4, :name "KvoOq", :type :add-cmd}
         {:id -6, :name "hWn", :type :add-cmd}
         {:id 6, :type :delete-cmd}
         {:id -4, :type :delete-cmd})],
 :shrunk {:total-nodes-visited 55, :depth 16, :result false,
          :smallest [({:id 0, :name "0", :type :add-cmd}
                      {:id -2, :name "2", :type :add-cmd}
                      {:id 0, :type :delete-cmd}
                      {:id -2, :type :delete-cmd})]}}

If you look closely the failing test case has three add commands, but when shrunk only two needed in order to fail appear.

Have fun!

I’m guilespi on Twitter.

Last year I attended Clojure/West in San Francisco, and was lucky enough to be at the talk by John Hughes, called Testing the hard stuff and staying sane.

I had been previously exposed to some of the concepts of generative testing, particularly Haskell’s own QuickCheck, but never took the time to do something with it, this talk by John Hughes really stroke a chord on the usefulness of generative -or property based- testing, and how much effort you can save by knowing when and how to use it.

I’ve been using Clojure test.check for a while, and since I’m preparing a conference talk on the subject, I decided to write something about it.

So bear with me, in this two-entry blog post I’ll try to convince you why down the road, it may save your ass too.

What generative testing is not

Probably the reason I’ve always looked down upon generative testing, was thinking it was just about random/junk data generation, for the too-lazy-to-think-your-own-test-cases kind of attitude.

Well, that’s not what generative testing is about.

You will have data generators for some input domain values, but trying to generate random noise to make the program fail is just fuzzy testing, and generative testing is more than that.

How?

On Types vs. Tests

I’ve written before about the difficulty of using types to prove your program is correct. Some people will always say you can do it with type systems(and types even more complex than the program under proof), and you can always use Coq.

But for everyday programming languages and type systems it’s not that easy, say for instance this Java function (assuming such thing exists).

1
2
3

int f1(int x) {
    return 1/x;
}

You can say just by looking at the function, that any integer except zero will succeed.

In this other case:

1
2
3

int f2(String x) {
    return x.length();
}

The function will succeed except when x is null.

So assuming that’s expected behavior, you can write some tests to check on those special failure cases.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

@Test(expected=ArithmeticException.class)
public void testDivideByZero() {
    f1(null);
}

//this is just a unit test
@Test
public void testUnity() {
    assertEquals(1, f1(1));
}

@Test(expected=NullPointerException.class)
public void testNullPointerException() {
    f2(null);
}

But for the sake of making and argument, assume you’re testing openssl and this is the function you have…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

int dtls1_process_heartbeat(SSL *s)
  {
    ...    
  /* Read type and payload length first */
  if (1 + 2 + 16 > s->s3->rrec.length)
      return 0; /* silently discard */
  hbtype = *p++;
  n2s(p, payload);
  if (1 + 2 + payload + 16 > s->s3->rrec.length)
      return 0; /* silently discard per RFC 6520 sec. 4 */
  pl = p;

  if (hbtype == TLS1_HB_REQUEST)
      {
      unsigned char *buffer, *bp;
      unsigned int write_length = 1 /* heartbeat type */ +
                      2 /* heartbeat length */ +
                      payload + padding;
      int r;

      if (write_length > SSL3_RT_MAX_PLAIN_LENGTH)
          return 0;

      /* Allocate memory for the response, size is 1 byte
      * message type, plus 2 bytes payload length, plus
      * payload, plus padding
      */
      buffer = OPENSSL_malloc(write_length);
      bp = buffer;

      /* Enter response type, length and copy payload */
      *bp++ = TLS1_HB_RESPONSE;
      s2n(payload, bp);
      memcpy(bp, pl, payload);
      bp += payload;
      /* Random padding */
      RAND_pseudo_bytes(bp, padding);
    ...

Unless you’ve been living under a rock, you should have heard about the heartbleed openssl bug, and it’s just what you think, the bug was in the heartbeat processing function above, and this is the patch with the fix.

Who was the motherfucker that missed that unit test, huh?

When the function logic is more complex, it’s exponentially more difficult to define both types and tests that make us feel more confident about pushing our nasty bits of code to a production environment.

And that’s because the possible states our system or function can be, expand like hell when new variables and conditional branches are added (more on this later).

Code Coverage vs. Domain Coverage

Looking at the function above you can see the problem is not on some untested code path, but on some values used on function invocation.

Some people aim for 100% code coverage, according to Wikipedia

In computer science, code coverage is a measure used to describe the degree to which the source code of a program is tested by a particular test suite. A program with high code coverage has been more thoroughly tested and has a lower chance of containing software bugs than a program with low code coverage.

Which is great, but since you can have 100% code coverage of the 1/x function, but regarding domain coverage (for which values of x the function works as expected) you have nothing.

Code coverage without domain coverage is just half the picture.

Even unit tests prove almost nothing.

Tests do not prove correctness

There’s a great quote by Edsger Dijkstra from Notes on Structured Programming that says

Program testing can be used to show the presence of bugs, but never to show their absence!

Which is to say, no matter how many unit tests you write, you’re only proving that your program works (or fails) for the set of inputs you have selected when writing your tests.

It doesn’t say a thing about the generalities or about a general property of the system or function under test.

What is generative testing?

So what is generative testing?

In generative testing you describe some properties your system or function must comply with, and the test runner provides randomized data to check if the property holds for that data, that’s why it’s also known as property-based testing.

A property is a high-level specification of behavior that should hold for a range of data points.

So a property works somewhat like a domain iterator, bringing a little bit closer types and tests.

Since you’re defining how the system should behave for a particular domain of values, not when the program is compiled, but when it’s run.

Why random data generation is important?

In the StrangeLoop 2014 conference, Joe Armstrong gave a talk called The mess we’re in, where he discussed system’s complexity, go watch it since it’s real fun.

He says that a C program with only six 32 bit integers, has the same number of states that atoms exist on the planet, so testing your program by computing all combinations it’s going to take a really long time.

And if it’s almost impossible to find the number of states computationally, imagine trying to find the number of possible failing states manually.

I’ve been in the position of having to hunt a bug that occurs only once a year in a system processing millions of transactions daily, and it’s not fun at all. Pray to the logging gods the proper piece of information revealing the culprit is logged, so you don’t have to wait another year for the bug to show up.

If your software runs inside a car, would you wait for the next deadly crash to analyze that dead-driver log file? Maybe that’s why Volvo uses QuickCheck to test embedded systems.

Generative testing helps you put and test your system in so many different states it would be impossible to do manually.

What’s in a property

So, should we throw away all of our type systems and unit tests?

Not so fast, property based testing is not a replacement for types nor for unit tests.

Haskell and Scala both have their frameworks for property based testing (QuickCheck and ScalaTest) and are strongly typed languages.

Property based testing helps us define considerations for our programs where type systems do not reach, and where dynamically typed languages have a void.

So what does a property look like?

All concepts so far hold true for any language with a generative testing framework, many re-implementations exist from the original QuickCheck version, from C, C++, Ruby, Clojure, Javascript, Java, Scala, etc. So now I will show you a couple of examples in different languages, just for you to grasp the basic property definition semantics, which is quite similar along the implementations.

These examples are not meant to show how powerful generative testing can be, yet.

Sorting in Javascript

Let’s say you want to test a sort function of yours, and instead of specifying individual test cases for particular arrays of integers, you define a property, which says that after sorting the array, the last element should always be greater than the first one.

This is what the property looks like in Javascript’s JSCheck

1
2
3
4
5
6
7
8
9
10
11

JSC.reps(10)
JSC.test(
    "First is lower than last after sort",
    function (verdict, v) {
        var sorted = v.sort();
        return verdict(sorted[0] < sorted[sorted.length - 1]);
    },
    [
        JSC.array([JSC.integer()]])
    ]
);

You don’t say which particular arrays, just any array of integers must comply with the property, the framework will generate values for you (in this case 10 repetitions will be run).

This is the result:

1
2
3
4

First is lower than last after sort: 10 cases tested, 0 pass, 10 fail
 FAIL [1] ([3])
 FAIL [2] ([5])
 FAIL [3] ([7])

Did you spot when the property doesn’t hold?

Sorting in Clojure

This is what the same property looks like in Clojure’s test.check.

1
2
3
4
5
6

(def prop-sorted-first-less-than-last
  (prop/for-all [v (gen/not-empty (gen/vector gen/int))]
    (let [s (sort v)]
      (< (first s) (last s)))))

(tc/quick-check 200 prop-sorted-first-less-than-last)

With the following result:

1
2
3

   => {:result false, :failing-size 0, :num-tests 1, :fail [[3]],
       :shrunk {:total-nodes-visited 5, :depth 2, :result false,
                :smallest [[0]]}}

As you see, both fail, since they doesn’t hold for single element arrays.

The basic semantic for both languages is the same, you need:

• A property name (or claim in JSCheck)
• Some data generator for your input values
• A verdict or testing function who validates the property

This encourages a higher level approach to testing in the form of abstract invariant functions should satisfy universally.

Shrinking

One of the best features of QuickCheck is the ability to shrink your failure cases to the minimum failing case (not all the implementations have it by the way).

When generating random data, you may end up with a failing case too big to rationalize (for instance a thousand elements vector), but it doesn’t necessarily means that all the 1000 elements are needed for the function under test to fail.

When QuickCheck finds a failing case, it tries to shrink the input data to the smallest failing case.

This is a powerful feature if you don’t want to repeat many unnecessary steps in order to reproduce a problem.

A simple example to illustrate the feature comes from test.check samples.

Here a property must hold for all integer vectors, and it is that no vector should have the element 42 in it.

1
2
3

(def prop-no-42
  (prop/for-all [v (gen/vector gen/int)]
    (not (some #{42} v))))

When the tests are run, test.check find a failing case being the vector [10 1 28 40 11 -33 42 -42 39 -13 13 -44 -36 11 27 -42 4 21 -39], which is not the minimum failing case.

1
2
3
4
5
6
7
8
9

(tc/quick-check 100 prop-no-42)
;; => {:result false,
       :failing-size 45,
       :num-tests 46,
       :fail [[10 1 28 40 11 -33 42 -42 39 -13 13 -44 -36 11 27 -42 4 21 -39]],
       :shrunk {:total-nodes-visited 38,
                :depth 18,
                :result false,
                :smallest [[42]]}}

So it starts shrinking the failing case until it reaches the smallest vector for which the property doesn’t hold, which is [42].

Unfortunately JSCheck doesn’t shrink the failure cases, but jsverify does, so if you want some shrinking on Javascript give it a try.

Final thoughts

Since QuickCheck depends on generators to cover the domain, we need to consider those domains may be infinite or very large, so it may be impossible to find the offending failure cases. None the less, we know that by running long enough or a large enough number of tests, we have better odds of finding a problem.

Regarding the name, property-based testing is a much better name than generative testing, since the later gives the idea that it’s about generating data, when it’s truly about function and system properties.

The higher level approach of property definition, coupled with the data generation and shrinking features provided by QuickCheck, really helps the case of having something more closer to proofs about how your system behaves.

In the next post I’ll write about finite state machine testing using test.check and show more complex examples, stay tuned.

I’m guilespi on Twitter, reach out!

This is the third entry in the Decompiling Clojure series.

In the first post I showed what Clojure looks like in bytecode, and in the second post I did a quick review of the Clojure compiler and its code generation strategies.

In this post I’ll go deeper in the decompiling process.

What is decompiling?

Decompilers do not usually reconstruct the original source code, since many information meant to be read by humans (for instance comments) is lost in the compilation process, where stuff is meant to be read only by machines, JVM bytecode in our case.

So by decompiling I mean going from lower level bytecode, to some higher level code, it doesn’t even need to be Clojure, we already know from the last post that Clojure compiler loses all macro information, so special heuristics will be needed when trying to reconstruct them.

For instance, it’s possible for let and if special forms, to be re-created using code signatures.(Think pattern matching applied to code graphs)

Decompiling goal

As I’ve said in my previous post:

What use do I have for a line based debugger with Clojure?

My goal when decompiling Clojure is not to re-create the original source code, but to re-create the AST that gave origin to the JVM bytecode I’m observing.

Since I was creating a debugger that knows about s-expressions, I needed a tree representation from the bytecode that can be properly synchronized with the Clojure source code I’m debugging.

So my decompiling goal was just getting a higher level semantic tree from the JVM bytecode.

Decompiling phases

Much of the work I’ve done was using as guide the many publications from Cristina Cifuentes, and the great book Flow Analysis of Computer Programs, which I got an used copy from Amazon. So all the smart ideas belong to them, all mistakes and nonsense are mine.

I already said I want a reasonable AST from the bytecode, so decompilation process will be split in phases

1. Wind the stack and build a statement list
2. Create codeblocks and a graph representing control flow
3. Detect loops and nested loops
4. Structure conditionals

If you want a decompiler that re-creates source code, you would add a fifth step called Emit source code.

As you smart readers would have probably noticed by now, it has some things in common with the compiling process, only that we need to get to the AST from compiled bytecode instead of doing it from a source file, once you have the AST you can emit whatever you want, even Basic.

1. Wind the stack

Maybe I should have used a different name for this step, since stack unwinding is usually related with C++ exception handling, and refers to how objects allocated are destroyed when exiting the function and destroying the frame.

But in the general case, stack unwind refers to what happens with the stack when a function is finished and the current frame needs to be cleared.

And if we go to the dictionary - pun intended -

to become uncoiled or disentangled

I’m happy to say we will coil the uncoiled stack into proper statements.

As we saw in the second post of our series, the JVM uses a stack based approach to parameter passing

1
2
3
4
5
6
7
8

f(a, b, c)

=> compiles to

push a
push b
push c
call f

So our first step is about getting the stack back together.

Some statements are going to be quite similar to what the Clojure compiler already recognizes, such as IfExpr representing an if conditional, but many statements at this stage won’t have a direct mapping in Clojure, for instance the AssignStatement representing an assignment to a variable, does not exist in the Clojure compiler, and higher level constructs such as LetFnExpr or MapExpr won’t be mapped at this stage of low-level bytecode.

So a reduced list would look like:

• AssignStatatement
• IfStatement
• InvokeStatement
• ReturnStatement
• NewStatement

So we’re dealing with less typed expressions/statements, just a small set of generic control structures.

One important thing when winding the stack is: in many cases statement compose, for instance an InvokeStatement result may be used directly from the stack into a subsequent IfStatement.

Let me show you.

Getting back to our previous example

1
2
3
4
5

(defn test-if
  []
  (if (= (inc 1) 2)
    8
    9))

Decompiled as

1
2
3
4
5
6
7
8
9
10
11
12
13
14

public java.lang.Object invoke();
    Code:
==>
       0: lconst_1
       1: invokestatic  #63                 // Method clojure/lang/Numbers.inc:(J)J
       4: ldc2_w        #42                 // long 2l
       7: lcmp
       8: ifne          18
==>
      11: getstatic     #49                 // Field const__4:Ljava/lang/Object;
      14: goto          21
      17: pop
      18: getstatic     #53                 // Field const__5:Ljava/lang/Object;
      21: areturn

Lines 0 and 1 are responsible for the (inc 1) part of the code, decompiling to clojure.lang.Numbers.inc(1), which result is directly used in line 7 which compares with the long value 2 pushed on line 4.

So our first decompiled statement on line 0 is an IfStatement, which contains the InvokeStatement inside.

1
2
3

0:IF (2!=clojure.lang.Numbers.inc(1)) GOTO 11 ELSE GOTO 18
11:RETURN 9
18:RETURN 8

When this step is finished all the low level concepts will be removed, and high level concepts were re-introduced, such as parameter passing.

But we’re still stuck with our damn Basic!

Codeblock Graph

A Codeblock is a sequence of statements with no branch statements in the middle, meaning execution starts at the first statement, and ends with the last one.

The following is a control flow graph, with code blocks numbered from B1 to B15.

Note we’re building a graph here, not a tree.

A tree is a minimally connected graph, having only one path between any two vertices, when modeling control flow you can have many paths between two vertices, for instance in our example B1->B2->B4->B5 and B1->B5.

This is the first step of the control flow analysis phase, having identified the basic branching statements from the previous step, building the graph is straightforward.

Loop Detection

Loop detection is one of the most difficult tasks when writing a decompiler.

Main reason is when you’re reading bytecode or assembly, you’re not entirely sure about the compiler used to generate that, you may be trying to decompile bytecode written by hand, which may never map to a known higher level construct.

For instance, there are a few higher level constructs identified with loops, which usually take the following form:

But then you may have a graph with the following improper looping structures:

Improper loops ranging from multi-entry or multi-exit, something you can find on goto enabled languages, to parallel loops with a common header node, or entwined loops.

In our case, we can assume all bytecode we’re going to find is always created from a reasonable Clojure compiler, and we can safely guess goto support won’t be approved by Rich Hickey any time soon.

So, a loop needs to be defined in terms of the graph representation, which not only determines the extent of the loop but also the nesting of the different loops in the function being decompiled.

The loop detection algorithms I used were taken directly from Cifuentes papers about decompiling, which in turn took the ideas from James F.Allen and John Cocke of using graph interval theory for flow analysis, since it satisfies the necessary conditions for loops:

• One loop per interval
• A nesting order is provided by the derived sequence of graphs.

Even if we don’t have improper loops, we need to know which IfStatements correspond to a loop header before assuming it’s indeed an If.

So, what does a Clojure loop looks like?

1
2
3
4
5

(defn test-loop
  []
  (loop [x 10]
    (when (> x 0)
      (recur (dec x)))))

Our first phase decompiler would see it as:

1
2
3
4
5

0:x = 10
4:IF (0<=x) GOTO 10 ELSE GOTO 22
10:x = clojure.lang.Numbers.dec(x)
15:GOTO 4
22:RETURN NULL

Well, we had a GOTO after all… as you see a loop is just an If statement followed by a backlink, in this case solved with a GOTO branching statement.

Now if I leave the debug comments from my decompiler, you’ll see a couple extra things:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Loading:debugee.test$test_loop

Block Start:0
0:x = 10

Block Start:4
4:IF (0<=x) GOTO 10 ELSE GOTO 22

Block Start:10
10:x = clojure.lang.Numbers.dec(x)
15:GOTO 4

Block Start:22
22:RETURN NULL

Found new loop header at:4
Not belong to loop:22
Loop closes on:10

• Code blocks are identified
• Loop belonging nodes are identified
• Loop header and latch nodes are also identified

Structuring Conditionals

Conditionals refer to if, when, case and other conditionals that may be found in code, which are usually 1-way or 2-way conditioned branches, all of them have a common end node reached by all paths.

Since Clojure when is a macro expanding to an if, it’s just the 1-way conditional branch, if the if clause has an else part we’re in the 2-way conditional branch, where the else part is taken before reaching the common follow node.

The more difficult situation arises when trying to structure compound boolean conditions, as you see in the following picture:

You should expect different IfStatements one behind the other, all being part of the same higher-level compound conditional which is compiled in a short-circuit fashion, with two chained if statements.

With Clojure we have an additional problem, for instance the following example:

1
2
3
4
5

(defn test-compound
  []
  (if (and (> 2 1) (= 0 0))
    2
    1))

Decompiles to the following Basic:

1
2
3
4
5
6

0:and__3941__auto__1754 = clojure.lang.Numbers.gt(2, 1)
8:IF and__3941__auto__1754==0 GOTO 12 ELSE GOTO 21
12:IF clojure.lang.Util.equiv(0, 0)==0 GOTO 25 ELSE GOTO 32
21:IF and__3941__auto__1754==0 GOTO 25 ELSE GOTO 32
25:RETURN 2
32:RETURN 1

Wait a minute!!

We should be seeing only two IfStatements there, one for each part of the compound conditional, but there are three, what’s going on?

As you see on line 21 the same condition of line 8 is being tested again, which we already know it’s false, why someone would do that?

It turns out it has to do with and being implemented as a macro, so if we look what’s the actual Clojure code being emitted the bytecode makes sense

1
2
3
4
5
6
7
8

(clojure.pprint/pprint
  (macroexpand-all '(if (and (> 2 1) (= 0 0)) 2 1)))
    (if
     (let*
       [and__3941__auto__ (> 2 1)]
       (if and__3941__auto__ (= 0 0) and__3941__auto__))
     2
     1)

The and__3941__auto__ variable which is the result of the first condition is being checked twice, I guess this is the reason the temporary variable exists in the first place, to avoid computation of the boolean expression twice and just checking for the result of it again.

If case the compiler analyzed the and as part of the if it could have emitted the result directly instead of using a temporary variable and that nasty double check.

The Clojure case

Many of the different strategies explored previously apply if you want to decompile just about anything from bytecode (or machine language).

Since in our case we already know we’re decompiling Clojure, there are a lot of special cases we know we will never encounter.

Targeting our decompiler to only one language makes things easier, since while we’re not only supporting only one compiler, but we know we’ll never encounter manually generated bytecode, unless your using an agent or custom loader that has patched the bytecode, of course.

What’s next

In the next post I will show you two things, how to synchronize the decompiled bytecode tree with Clojure source code, and how to patch the debuggee on runtime to use our s-expression references using BCEL.

Much of the code to accomplish this was developed while understanding the problem, so it’s not open sourced yet, I’m planning to move stuff around and make it public, but if you want to look at the current mess just ping me, I’ll send it to you(you’ll need to un-rust your graph mangling skills tough).

Meanwhile, I’m guilespi on Twitter.

This is the second post in the Decompiling Clojure series, in the first post I showed what Clojure looks like in bytecode.

For this entry, I’ll do a compiler overview, the idea is to understand why and how does Clojure looks like that.

For other decompilation scenarios you don’t usually have the advantage of looking at the compiler internals to guide your decompiling algorithms, so we’ll take our chance to peek at the compiler now.

We will visit some compiler source code, so be warned, there’s Java ahead.

It’s Java

Well, yes, the Clojure compiler targeting the JVM is written in Java, there is an ongoing effort to have a Clojure-in-Clojure compiler, but the original compiler is nowhere near of being replaced.

The source code is hosted on GitHub, but the development process is a little bit more convoluted, which means you don’t just send pull requests for it, it was asked for many times and I don’t think it’s about to change, so if you wanna contribute, just sign the contributors agreement and follow the rules.

The CinC Alternative

The Clojure-in-Clojure alternative is not only different because it’s written in Clojure, but because it’s built with extensibility and modularization in mind.

In the original Clojure compiler you don’t have a chance to extend, modify or use, many of the data produced by the compilation process.

For instance the Typed Clojure project, which adds gradual typing to Clojure, needed a friendlier interface to the compiler analyzer phase. It was first developed by Ambrose Bonnair-Sergeant as an interface to the Compiler analyzer and then moved to be part of the CinC analyzer.

The CinC alternative is modularized in -at least three- different parts.

• The analyzer, meant to be shared among all Clojure compilers (as Clojurescript)
• The JVM analyzer, contains specific compiler passes for the JVM (for instance locals clearing is done here)
• The bytecode emitter, actually emits JVM bytecode.

There’s a great talk from Timothy Baldridge showing some examples using the CinC analyzer, watch it.

Note CinC developer Nicola Mometto pointed out that the analyzer written by Ambrose and CinC are indeed different projects. Which I should’ve noticed myself since the analyzer by Ambrose uses the analyzer from the original Clojure compiler, which is exposed as a function. Part of my mistake was surely derived from the fact one is called tools.analyzer.jvm and the other one is called jvm.tools.analyzer

Compilation process

One of supposed advantages of Lisp-like languages is that the concrete syntax is already the abstract syntax. If you’ve read some of the fogus writings about Clojure compilation tough, he has some opinions on that statement:

This is junk. Actual ASTs are adorned with a boatload of additional information like local binding information, accessible bindings, arity information, and many other useful tidbits.

And he’s right, but there’s one more thing, Clojure and Lisp syntax are just serialization formats, mapping to the underlying data structure of the program.

That’s why Lisp like languages are easier to parse and unparse, or build tools for them, because the program data structure is accesible to the user and not only to the compiler.

Also that’s the reason why macros in Lisp or Clojure are so different than macros in Scala, where the pre-processor handles you an AST that has nothing to do with the Scala language itself.

That’s the proper definition of homoiconicity by the way, the syntax is isomorphic with the AST.

Compiler phases

In general compilers can be broken up into three pieces

1. Lexer/Parser
2. Analyzer
3. Emitter

Clojure kind of follows this pattern, so if we’re compiling a Clojure program the very high level approach to the compilation pipeline would be:

1. Read file
2. Read s-expression
3. Expand macros if present
4. Analyze
5. Generate JVM bytecode

The first three steps are the Reading phase from the fogus article.

There is one important thing about these steps:

Bytecode has no information about macros whatsoever, emitted bytecode corresponds to what you see with macroexpand calls. Since macros are expanded before analyzing, you shouldn’t expect to find anything about your macro in the compiled bytecode, nada, niet, gone.

Meaning, we shouldn’t expect to be able to properly decompile macro’ed stuff either.

Compile vs. Eval

As said on the first post, the class file doesn’t need to be on disk, and that’s better understood if we think about eval.

When you type a command in the REPL it needs to be properly translated to bytecode before the JVM is able to execute it, but it doesn’t mean the compiler will save a class file, then load it, and only then execute it.

It will be done on the fly.

We will consider three entry points for the compiler, compile, load and eval.

The LispReader is responsible for reading forms from an input stream.

Compile Entry Point

compile is a static function found in the Compiler.java file, member of the Compiler class, and it does generate a class file on disk for each function in the compiled namespace.

For instance it will get called if you do the following in your REPL

1

(compile 'clojure.core.reducers)

Clojure function just wraps over the Java function doing the actual work with the signature

1

public static Object compile(Reader rdr, String sourcePath, String sourceName) throws IOException{

Besides all the preamble, the core of the function is just a loop which reads and calls the compile1 function for each form found in the file.

1
2
3
4
5

for(Object r = LispReader.read(pushbackReader, false, EOF, false); r != EOF;
          r = LispReader.read(pushbackReader, false, EOF, false))
  {
       compile1(gen, objx, r);
  }

As we expect, the compile1 function does macro expansion before analyzing or emitting anything, if form turns out to be a list it recursively calls itself, which is the then branch of the if test:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

form = macroexpand(form);
if(form instanceof IPersistentCollection && Util.equals(RT.first(form), DO))
  {
  for(ISeq s = RT.next(form); s != null; s = RT.next(s))
  {
      compile1(gen, objx, RT.first(s));
  }
  }
else
  {
  Expr expr = analyze(C.EVAL, form);
        ....
  expr.emit(C.EXPRESSION, objx, gen);
  expr.eval();
  }

The analyze function we see on the else branch does the proper s-expr analyzing which emits and evals itself afterwards, more on analyzing ahead.

Load Entry Point

The load function gets called any time we do a require for a not pre-compiled namespace.

1

public static Object load(Reader rdr, String sourcePath, String sourceName) {

For instance, say we do a require for the clojure.core.reducers namespace:

1

(require '[clojure.core.reducers :as r])

The clj file will be read as a stream in the loadResourceScript function and passed as the first rdr parameter of the load function.

You see the load function has a pretty similar read form and eval loop as the one we saw in the compile function.

1
2
3
4
5

for(Object r = LispReader.read(pushbackReader, false, EOF, false); r != EOF;
r = LispReader.read(pushbackReader, false, EOF, false))
{
  ret = eval(r,false);
}

Instead of calling compile1 calling eval, which is our next entry point.

Eval Entry Point

eval is the e in REPL, anything to be dynamically evaluated goes through the eval function.

For instance if you type (+ 1 1) on your REPL that expression will be parsed, analyzed and evaluated starting on the eval function.

1

public static Object eval(Object form, boolean freshLoader)

As you see eval receives a form by parameter, since knows nothing about files nor namespaces.

eval is just straightforward analyzing of the form, and there’s not a emit here. This is the simplified version of the function:

1
2
3

form = macroexpand(form);
Expr expr = analyze(C.EVAL, form);
return expr.eval();

The reader

Languages with more complicated syntaxes separate the Lexer and Parser into two different pieces, like most Lisps, Clojure combines these two into just a Reader.

The reader is pretty much self contained in LispReader.java and its main responsibility is given a stream, return the properly tokenized s-expressions.

The reader dispatches reading to specialized functions and classes when a particular token is found, for instance ( dispatches to ListReader class, digits dispatch to the readNumber function and so on.

Much of the list and vector reading classes(VectorReader, MapReader, ListReader, etc) rely on the more generic readDelimitedList function which receives the particular list separator as parameter.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

macros['"'] = new StringReader();
macros[';'] = new CommentReader();
macros['\''] = new WrappingReader(QUOTE);
macros['@'] = new WrappingReader(DEREF);//new DerefReader();
macros['^'] = new MetaReader();
macros['`'] = new SyntaxQuoteReader();
macros['~'] = new UnquoteReader();
macros['('] = new ListReader();
macros[')'] = new UnmatchedDelimiterReader();
macros['['] = new VectorReader();
macros[']'] = new UnmatchedDelimiterReader();
macros['{'] = new MapReader();
macros['}'] = new UnmatchedDelimiterReader();
//   macros['|'] = new ArgVectorReader();
macros['\\'] = new CharacterReader();
macros['%'] = new ArgReader();
macros['#'] = new DispatchReader();

This is important because the reader is responsible for reading line and column number information, and establishing a relationship between tokens read and locations in the file.

One of the main drawbacks of the reader used by the compiler is that much of the line and column number information is lost, that’s one of the reasons we saw in our earlier post that for a 7 line function only one line was properly mapped, interestingly, the line corresponding to the outter s-expression.

We will have to modify this reader if we want proper debugging information for our debugger.

The analyzer

The analyzer is the part of the compiler that translates your s-expressions into proper things to be emitted.

We’re already familiar with the REPL, in the eval function analyze and emit are combined in a single step, but internally there’s a two step process.

First, our parsed but meaningless code needs to be translated into meaningful expressions.

In the case of the Clojure compiler all expressions implement the Expr interface:

1
2
3
4
5
6

interface Expr{
  Object eval() ;
  void emit(C context, ObjExpr objx, GeneratorAdapter gen);
  boolean hasJavaClass() ;
  Class getJavaClass() ;
}

Much of the Clojure special forms are handled here, IfExpr, LetExpr, LetFnExpr, RecurExpr, FnExpr, DefExpr, CaseExpr, you get the idea.

Those are nested classes inside the Compiler class, and for you visualize how many of those special cases exist inside the compiler, I took this picture for you:

As you would expect for a properly modularized piece of software, each expression knows how to parse itself, eval itself, and emit itself.

The analyze function is a switch on the type of the form to be analyzed, just for you to get a taste:

1
2
3
4
5
6
7
8
9
10
11
12
13

private static Expr analyze(C context, Object form, String name) {

...

if(fclass == Symbol.class)
  return analyzeSymbol((Symbol) form);
else if(fclass == Keyword.class)
  return registerKeyword((Keyword) form);
else if(form instanceof Number)
  return NumberExpr.parse((Number) form);
else if(fclass == String.class)
  return new StringExpr(((String) form).intern());
...

And there’s special handling for the special forms which are keyed by Symbol on the same file.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

IPersistentMap specials = PersistentHashMap.create(
      DEF, new DefExpr.Parser(),
      LOOP, new LetExpr.Parser(),
      RECUR, new RecurExpr.Parser(),
      IF, new IfExpr.Parser(),
      CASE, new CaseExpr.Parser(),
      LET, new LetExpr.Parser(),
      LETFN, new LetFnExpr.Parser(),
      DO, new BodyExpr.Parser(),
      FN, null,
      QUOTE, new ConstantExpr.Parser(),
      THE_VAR, new TheVarExpr.Parser(),
      IMPORT, new ImportExpr.Parser(),
      DOT, new HostExpr.Parser(),
      ASSIGN, new AssignExpr.Parser(),
      DEFTYPE, new NewInstanceExpr.DeftypeParser(),
      REIFY, new NewInstanceExpr.ReifyParser(),

Analyze will return a parsed Expr, which is now a part of your program represented in the internal data structures of the compiler.

The bytecode generator

As said before it uses ASM so we found the standard code stacking up visitors, annotations, methods, fields, etc.

I won’t enter here into specific details about ASM API since it’s properly documented somewhere else.

Only notice that no matter if code is eval’ed or not, JVM bytecode will be generated.

What’s next

One of the reasons I ended up here when I started working on the debugger was to see if by any means, I could add better line number references to the current Clojure compiler.

As said before and as we saw here, the Java Clojure Compiler is not exactly built for extensibility.

The option I had left, was to modify the line numbers and other debugging information at runtime, and that’s what I will show you on the next post.

I will properly synchronize Clojure source code with JVM Bytecode, meaning I will synchronize code trees, that way I will not only add proper line references, but I will know which bytecode corresponds with which s-expression in your source.

Doing Clojure I usually end up with lines of code looking like this:

1

(map (comp first rest (partial filter identity)) (split-line line separator))

What use do I have for a line base debugger with that code??

I want an s-expression based debugger, don’t you?

One more reason we have to envy Dr Racket, whose debugger already knows about them.

Stay tuned to see it working on the JVM.

Meanwhile, I’m guilespi on Twitter.

This is the first in a series of articles about decompiling Clojure, that is, going from JVM bytecode created by the Clojure compiler, to some kind of higher level language, not necessarily Clojure.

This article was written in the scope of a larger project, building a better Clojure debugger, which I’ll probably blog about in the future.

These articles are going to build form the ground up, so you may skip forward if you find some of the stuff obvious.

Clojure targets the JVM

To be more precise, there is a Clojure compiler targeting the JVM, there’s also one targeting Javascript, one for the CLR and there are some less known projects targeting lua or even C.

But the official clojure core efforts are mainly on the JVM, which stands for Java Virtual Machine.

That means when you write some clojure code:

1
2
3

(ns hello-world)

(println "Hello World")

You won’t get a native binary, for instance a x86 PE or ELF file, although it’s entirely possible to write a compiler to do it.

When you target a particular runtime though, you usually get a different set of functions to interact with the host, there’s a lot of language primitives just to deal with Java inter operation which do not migrate easily to other runtimes or virtual machines.

The JVM is about Java, or is it?

This doesn’t mean that the JVM can only run programs written in Java.

In fact, Clojure doesn’t use Java as an intermediate language before compiling, the Clojure compiler for the JVM generates JVM bytecode directly using the ASM library.

So, what does it mean the JVM is about Java if you can compile directly to bytecode without a mandatory visit to the kingdom of nouns?

Besides its name, the JVM was designed by James Gosling in 1992 to support the Oak Programming Language, before evolving into its current form.

Its main responsibility is to achieve independence from hardware and operating system, and like a real machine, it has an instruction set and manipulates memory at runtime, and the truth is the JVM knows nothing about the Java Programming Language, it only knows of a particularly binary format, the class file format, which contains bytecode and other information.

So, any programming language with features that can be expressed in terms of a valid class file, can by hosted on the JVM.

But the truth is that the class file format, maintains a lot of resemblance with concepts appearing in Java, or any other OO programming language as a matter of fact, to name a few:

• A class file corresponds to a Class
• A class file has members
• A class file has methods
• Methods of the class file can be static or instance methods
• There are primitive types and reference types, that can be stored in variables
• Exceptions are an instance or subclass of Throwable
• etc

So, we can say the JVM is not agnostic regarding the concepts supported by the language, as the LISP machines were not agnostic either.

Clojure compiles to bytecode

So we have a language like Clojure, with many concepts not easily mapped to the JVM spec, but that it was mapped none the less, how?

Namespaces do not exist

Maybe you think Clojure namespaces correspond to a class, and each method in the namespace is mapped to a method in the class.

Well, that is not the case.

Namespaces were criticized before for being tough, and the truth is they’re used for proper modularity, but do not map to an entity in the JVM. They’re equivalent to java packages or modules in other languages.

Each function is a class

Each function in your namespace will get compiled to a complete different class. That’s something you can easily confirm listing the files under target/classes in a leiningen project directory.

1
2
3
4
5
6
7
8
9
10
11
12

git:(master) ✗ ls target/classes/

config$fn__292.class
routes__init.class
config$loading__4910__auto__.class
config$read_environment$fn__300.class
config$read_environment.class
config$read_properties$iter__304__308$fn__309$fn__310.class
server
server$_main.class
server$_main$fn__4006.class
server$fn__3939.class

You will find a .class file for each function you have defined, namespace$function.class being the standard syntax.

Each anonymous function is also a class

As you saw in the previous listing, there are many functions with numbers like config$fn__292.class.

Those correspond to anonymous functions that get their own class when compiled, so if you have this code:

1

(map #(+ 34 %) (range 10))

You should expect a .class file for the anonymous function #(+ 34 %).

class files don’t need to be on disk

Many times you’ll find the class files on disk, but it doesn’t have to be that way.

In many circumstances we’re going to be modifying the class structure on runtime, or creating new class structures to be run, entirely on memory. Even the compiler can eval some code compiling to memory without creating a class file on disk.

What does bytecode look like?

For the first example, I selected a real simple clojure function

1
2
3
4
5
6
7

(defn test-multi-let
  []
  (let [a 1
        b 2
        c 3
        b 4]
    9))

To explore the bytecode we will use javap, simple, but does the job:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

javap -c target/classes/debugee/test\$test_multi_let.class
...
public static {};
    Code:
       0: lconst_1
       1: invokestatic  #19                 // Method java/lang/Long.valueOf:(J)Ljava/lang/Long;
       4: putstatic     #21                 // Field const__0:Ljava/lang/Object;
       7: ldc2_w        #22                 // long 2l
      10: invokestatic  #19                 // Method java/lang/Long.valueOf:(J)Ljava/lang/Long;
      13: putstatic     #25                 // Field const__1:Ljava/lang/Object;
      16: ldc2_w        #26                 // long 3l
      19: invokestatic  #19                 // Method java/lang/Long.valueOf:(J)Ljava/lang/Long;
      22: putstatic     #29                 // Field const__2:Ljava/lang/Object;
      25: ldc2_w        #30                 // long 4l
      28: invokestatic  #19                 // Method java/lang/Long.valueOf:(J)Ljava/lang/Long;
      31: putstatic     #33                 // Field const__3:Ljava/lang/Object;
      34: ldc2_w        #34                 // long 9l
      37: invokestatic  #19                 // Method java/lang/Long.valueOf:(J)Ljava/lang/Long;
      40: putstatic     #37                 // Field const__4:Ljava/lang/Object;
      43: return

I’ve removed some extra information such as variable tables, we’re going to be visiting those later.

What you see here are JVM assembly instructions, just a subset of the JVM instruction set, generated by the Clojure compiler when feed with the sample function above.

Before we get into more details, let me show you how that code looks after a basic decompiler pass:

1
2
3
4
5

0:a = 1
2:b = 2
6:c = 3
11:b = 4
16:RETURN 9

Prettier uh?

That is until you decompile this:

1
2
3
4
5

(defn test-if
  []
  (if (= (inc 1) 2)
    8
    9))

And get this:

1
2
3

0:IF (2 != clojure.lang.Numbers.inc(1)) GOTO 11 ELSE GOTO 18
11:RETURN 9
18:RETURN 8

Who was the moron that put a BASIC in my Clojure!

Ain’t it?

Keep reading… there’s more to be seen ahead.

The operand stack

I won’t dwell into many details about each JVM instruction and how that translates to something resembling Clojure, or Basic for that matter, but there’s one thing worth of mention, and that is the operand stack.

Frames

A new Frame is created each time a method is invoked and destroyed when the method completes, whether that information is normal or abrupt (throws an uncaught exception), frames are allocated in the JVM stack and have its own array of local variables and its own operand stack.

If you set a breakpoint on your code, each different entry in your thread callstack, is a frame.

Stack

The operand stack is a last-in-first-out (LIFO) stack and its empty when the Frame that contains it is created, and the JVM provides instructions for loading constants or variables into the operand stack, and to put values from the operand stack in variables.

The operand stack is usually used to prepare parameters to be passed to methods and to receive method results, as opposed to using registers to do it.

So you should expect something along these lines:

1
2
3
4
5
6
7
8

f(a, b, c)

=> compiling to

push a
push b
push c
call f

So looking again at the bytecode of the previous function:

1
2
3
4
5

(defn test-if
  []
  (if (= (inc 1) 2)
    8
    9))

Here:

1
2
3
4
5
6
7
8
9
10
11
12

public java.lang.Object invoke();
    Code:
       0: lconst_1
       1: invokestatic  #63                 // Method clojure/lang/Numbers.inc:(J)J
       4: ldc2_w        #42                 // long 2l
       7: lcmp
       8: ifne          18
      11: getstatic     #49                 // Field const__4:Ljava/lang/Object;
      14: goto          21
      17: pop
      18: getstatic     #53                 // Field const__5:Ljava/lang/Object;
      21: areturn

We can make ourselves an interpretation about what’s going on…

lconst_1 is pushing the constant value 1 into the stack, then calling a static method with invokestatic, as you’ve already guessed that’s the clojure.lang.Numbers.inc(1) we saw on the basic decompiler earlier.

Then ld2_w loads the value 2 into the stack and lcmp will compare it against the function result, ifne tests for non equality and jumps to line 18 if values differ.

One thing to consider here is that each entry on the operand stack can hold a value of any JVM type, and those must be operated in ways appropriate to their types, so many operations have a different operation code according to the type they’re handling.

So looking at this example from the JVM specification, we see the operations are prefixed with a d since they operate on double values.

1
2
3
4
5

Method double doubleLocals(double,double)
0 dload_1 // First argument in local variables 1 and 2
1 dload_3 // Second argument in local variables 3 and 4
2 dadd
3 dreturn

Which as you may have guessed, is adding double values 1 and 3.

JVM auxiliary information

The JVM class format has support for some extra information that can be used for debugging purposes, some of which you can get rid from your files if you want.

Among those we find the LineNumberTable attribute and the the LocalVariableTable attribute, which may be used by debuggers to determine the value of a given local variable during the execution of a method.

According to the jvm spec, the table has the following structure inside the class file format

1
2
3
4
5
6
7
8
9
10
11

LocalVariableTable_attribute {
       u2 attribute_name_index;
       u4 attribute_length;
       u2 local_variable_table_length;
       {   u2 start_pc;
           u2 length;
           u2 name_index;
           u2 descriptor_index;
           u2 index;
       } local_variable_table[local_variable_table_length];
   }

Basically it says which variable starts at which instruction: start_pc and lasts for how long: length.

If we look at that table for our let example:

1
2
3
4
5
6
7

(defn test-multi-let
  []
  (let [a 1
        b 2
        c 3
        b 4]
    9))

We see how each variable is referenced against program counter(pc) line numbers (do not get confused with source file line numbers).

1
2
3
4
5
6
7

LocalVariableTable:
      Start  Length  Slot  Name   Signature
             2      17     1     a   J
             6      13     3     b   J
            11       8     5     c   J
            16       3     7     b   J
             0      19     0  this   Ljava/lang/Object;

One interesting thing though, is the LineNumberTable

1
2
3

  public debugee.test$test_multi_let();
    LineNumberTable:
      line 204: 0

Which has only one line number reference, even if our function was 7 lines long, obviously that cannot be good for a debugger expecting to step over each line!

Next post I’ll blog about the Clojure compiler and how it ends up creating that bytecode, before visiting again the decompiling process.

I’m guilespi on Twitter, get in touch!

This post is about Clojure reducers, but what makes them great are the ideas behind the implementation, which may be portable to other languages.

So if you’re interested in performance don’t leave just yet.

One of the primary motivators for the reducers library is Guy Steele’s ICFP ‘09 talk, and since I assume you don’t have one hour to spend verifying I’m telling you it’s worth watching, I’ll do my best to summarize it here, which is a post you will probably scan in less than 15 seconds.

One of the main points of the talk is that the way we’ve been thinking about programming for the last 50 years isn’t serving us anymore.

Why?

Because good sequential code is different from good parallel code.

Parallel vs. Sequential

1
2
3
4
5
6
7

+------------+--------------------------------------+-------------------------------------------------------------+
|            |              Sequential              |                          Parallel                           |
+------------+--------------------------------------+-------------------------------------------------------------+
| Operations | Minimizes total number of operations | Often performs redundant operations to reduce communication |
| Space      | Minimize space usage                 | Extra space to permit temporal decoupling                   |
| Problem    | Linear problem decomposition         | Multiway aggregation of results                             |
+------------+--------------------------------------+-------------------------------------------------------------+

The accumulator loop

How would you sum all the elements of an array?

1
2
3
4

SUM = 0 
DO I = 1, 1000000
   SUM = SUM + X(I)
END DO

That’s right, the accumulator loop, you initialize the accumulator and update the thingy in each iteration step.

But you’re complecting how you update your sum with how you iterate your collection, ain’t it?

There’s a difference between what you do with how you do it. If you say SUM(X) it doesn’t make promises on the strategy, it’s when you actually implement that SUM that the sequential promise is made.

The problem is the computation tree for the sequential strategy, if we remove the looping machinery and leave only the sums, there’s a one million steps delay to get to the final result.

So what’s the tree you would like to see?

And what code you would need to write in order to get that tree? Functional code?

Think again.

Functional code is not the complete answer, since you can write functional code and still have the same problem.

Since linear linked lists are inherently sequential you may be using a reducer and be on the same spot.

1

(reduce + (range 1 1000000))

We need multiway decomposition.

Divide and conquer

Rationale behind multiway decomposition is that we need a list representation that allows for binary decomposition of the list.

You can obviously have many redundant trees representing the same conceptual list, and there’s value in redundancy since different trees have different properties.

Summary

• Don’t split a problem between first and rest, split in equal pieces.
• Don’t create a null solution an successively update it, map inputs to singleton solutions and merge tree-wise.
• Combining solutions is trickier than incremental updates.
• Use sequential techniques near the leaves.
• Programs organized for parallelism can be processed in parallel or sequentially.
• Get rid of cons.

Clojure Reducers

So what are Clojure reducers?

In short, it’s a library providing a new function fold, which is a parallel reduce+combine that shares the same shape with the old sequence based code, main difference been you get to provide a combiner function.

Go and read this and this great posts by Rich Hickey.

Back? Ok…

As Rich says in his article the accumulator style is not absent but the single initial value and the serial execution promises of foldl/r have been abandoned.

For what it’s worth, I’ve written in Clojure the Split a string into words parallel algorithm suggested by Steele here, performance sucks compared against clojure.string/split but it’s a nice algorithm none the less.

1
2
3
4
5
6
7
8

(defn parallel-words
  [w]
  (to-word-list
   (r/fold 100
           combine-states
           (fn [state char]
             (append-state state (process-char char)))
           (vec (seq w)))))

There are a couple interesting things in the code.

• combine-states is the new combiner function, decides how to combine different splits
• 100 is the size when to stop splitting and do a sequential processing (calls reduce afterwards). Defaults to 512.
• The fn is the standard reducing function
• The list is transformed into a vector before processing.

Last step is just for the sake of experimentation, and has all to do with the underlying structure for vectors.

Both vectors and maps in Clojure are implemented as trees, which as we saw above, is one of the requirements for multiway decomposition. There’s a great article here about Clojure vectors, but key interest point is that it provides practically O(1) runtime for subvec, which is how the vector folder foldvec successively splits the input vector before reaching the sequential processing size.

So if you look at the source code only for vectors and maps actual fork/join parallelism happens, and standard reduce is called for linear lists.

1
2
3
4
5
6
7
8
9
10

 clojure.lang.IPersistentVector
 (coll-fold
  [v n combinef reducef]
  (foldvec v n combinef reducef))

 Object
 (coll-fold
  [coll n combinef reducef]
  ;;can't fold, single reduce
  (reduce reducef (combinef) coll))

What I like the most about reducers is that reducer functions are curried, so you can compose them together as in:

1
2
3

(def red (comp (r/filter even?) (r/map inc)))
(reduce + (red [1 1 1 2]))
;=> 6

It’s like the utmost example of the simple made easy Hickey’s talk, where decomplecting the system, results in a much simpler but powerful design at the same time.

I’m guilespi at Twitter

When you have a system with many moving parts it’s usually difficult trying to understand which one of those pieces is the culprit, say for instance your home page is taking 3 seconds to render and you’re losing customers, what the hell is going on?

Whether you’re using Memcache, Redis, RabbitMQ or a custom distributed service, if you’re trying to scale your shit up, you probably have many pieces or boxes involved.

At least that’s what happens at Twitter, so they’ve come up with a solution called Zipkin to trace distributed operations, that is, an operation that is potentially solved using many different nodes.

Twitter Architecture

Having dealt with distributed logging in the past, reconstructing a distributed operation from logs, it’s like trying to build a giant jigsaw puzzle in the middle of a Tornado.

The standard strategy is to propagate some operation id and use it anywhere you want to track what happened, and that is the essence of what Zipkin does, but in a structured kind of way.

Zipkin

Zipkin was modelled after Google Dapper paper on distributed tracing and basically gives you two things:

• Trace Collection
• Trace Querying

Zipkin Architecture

The architecture looks complex but it ain’t that much, since you can avoid using Scribe, Cassandra, Zookeeper and pretty much everything related to scaling the tracing platform itself.

Since the trace collector speaks the Scribe protocol you can trace directly to the collector, and you can also use local disk storage for tracing and avoid a distributed database like Cassandra, it’s an easy way to get your feet wet without having to setup a cluster to peek a few traces.

Tracing

There are a couple entities involved in Zipkin tracing which you should know before moving forward:

Trace

A trace is a particular operation which may occur in many different nodes and be composed on many different Spans.

Span

A span represents a sub-operation for the Trace, it can be a different service or a different stage in the operation process. Also, spans have a hierarchy, so a span can be a child of another span.

Annotation

The annotation is how you tag your Spans to actually know what happened, there are two type of spans:

• Timestamp
• Binary

Timestamp spans are used for tracing time related stuff, and Binary annotations are used to tag your operation with a particular context, which is useful for filtering later.

For instance you can have a new Trace for each home page request, which decomposes in the Memcache Span the Postgres Span and the Computation Span, each of those with their particular Start Annotation and Finish Annotation.

API

Zipkin is programmed in Scala and uses thrift, since it’s assumed you’re going to have distributed operations, the official client is Finagle, which is kind of a RPC system for the JVM, but at least for me, it’s quite ugly.

Main reason is that it makes you feel that if you want to use Zipkin you must use a Distributed Framework, which is not at all necessary. For a moment I almost felt like Corba and DCOM were coming back from the grave trying to lure me into the abyss.

There’s also libraries for Ruby and Python but none of them felt quite right to me, for Ruby you either use Finagle or you use Thrift, but there’s no actual Zipkin library, for Python you have Tryfer which is good and Restkin which is a REST API on top of it.

Clojure

In the process of understanding what Zipkin can do for you (that means me) I hacked a client for Clojure using clj-scribe and clj-thrift which made the process almost painless.

It comes with a ring handler so you can trace your incoming requests out of the box.

1
2
3
4
5
6
7
8
9
10

 (require '[clj-zipkin.middleware :as m])

   (defroutes routes
     (GET "/" [] "<h1>Hello World</h1>")
     (route/not-found "<h1>Page not found</h1>"))

   (def app
       (-> routes
       (m/request-tracer {:scribe {:host "localhost" :port 9410}
                          :service "WebServer"})))

Zipkin Web Analyzer

It’s far from perfect, undocumented and incomplete, but at least it’s free :)

Give it a try and let me know what you think.

I’m guilespi at Twitter

For some time now, tech industry has taken an active role in trying to solve the gender imbalance problem.

• Organizing conferences for women or by women
• Trying to bring more women into math or cs
• Offering grants and scholarships for Hacker School
• Public scorn for offenders when deserved
• Anti-Harassment policies for conferences

There’s even gender studies in mathematics and other sciences.

But even if the issue has been on the table for a while, I’ve attended a few conferences where I live and the usual attendance looks like this:

I don’t think you’ll find more than 5 women in the picture.

And I can tell you for sure, that picture does not represent at all the women in tech in the city. There may be an imbalance, but women are not by any means, 0,5% of computer science graduates here.

So women are not participating, but why?

The Data

Since StackExchange has open data you can derive some insights from, I decided to take a look at the problem from a different perspective, and address the question of the underrepresentation using StackOverflow data.

I started with a few questions in mind:

• What % of users are women?
• What’s the question/answer rate for men and women?
• How the reputation score for men and women compares?
• How it compares to ambiguous/unisex names?
• Is in fact SO a gentleman’s club?

Since SO has no gender data, gender needs to be inferred from user names, which is obviously not 100% accurate, many names are unisex or depend on the country of origin. I decided to use this database and program which has names from all over the world curated by local people. In many cases you will get a statistical result: mostly male or mostly female, and that makes sense.

Be warned this is not a scientific study nor tries to be, just trying to see some patterns here.

First Glimpse

First I wanted to get a glimpse of the general trends, so I did a random draw of 50k users, more than enough for what I need.

1
2

Select * From users
Order By newid()

StackExchange limits the number of rows returned by the online database browser to 50k, so that’s it.

1
2
3

  > table(users$gender)/nrow(users)
  anonymous    error in name        is female          is male     is mostly female   is mostly male   is unisex name   name not found
   0.25662       0.00006              0.02910          0.23640          0.00946          0.04654          0.02942          0.39240

As you see there’s a 27% of confirmed males and only a 4% of confirmed females. Anonymous users are the usual numerical users like user395607, and name not found refers to things like ppkt, HeTsH, holden321 and ITGronk, you get the idea.

Then I wanted to see how reputation was distributed among those users, and how that compared against how long the user was using the site.

There you go, an image is worth a thousand words, reputation difference among genders is huge, it doesn’t seem to be related to how long you’ve been around either.

Fresh users

To confirm that, I drew randomly 50k fresh users, who joined the site after 2012-10-10, just to see if trends were any different considering only last year data.

1
2
3

Select * From users
Where CreationDate > '2012-10-10'
Order By newid()

1
2
3

> table(users$gender)/nrow(users)
   anonymous    error in name        is female          is male     is mostly female   is mostly male   is unisex name   name not found
     0.35620      0.00002             0.03178          0.20320          0.01014            0.04076          0.02544         0.33246

Here women seem to be a little bit closer, but still a great difference.

The best of the best

Then I drew the 50k users with the highest reputation score.

1
2

Select * From users
Order By Reputation Desc

Now we’re seeing some changes:

1
2
3

> table(users$gender)/nrow(users)
   anonymous    error in name        is female          is male is mostly female   is mostly male   is unisex name   name not found
     0.00794          0.00002          0.01064          0.34130          0.00890          0.06656          0.03524          0.52940

As you expect here there’s almost no anonymous users, in the online community charity has a name attached to it, ain’t it?

And the reputation trend is still there, something you can readily confirm if you scroll the first pages of the all time user’s reputation page.

But then I charted the reputation distribution against gender and something interesting arises:

As you see, there’s a great deal of outliers there, with 75% of the top 50k users below 4200 points.

1
2
3

> quantile(users$reputation)
       0%       25%       50%       75%      100%
  1024.00   1415.00   2178.00   4214.25 618862.00

So what happens when we look at the distribution considering the 75% of the users, that are in fact below 4215 points?

Well that’s something! Now distribution looks pretty much alike.

Seems to me those outliers, that are mostly men, are well beyond everyone else, men or women.

How do you read that data?

Wrap up

At 4% females, SO seems to be suffering the same phenomena occurring in the real world, that is, women being underrepresented, but being SO a strongly moderated virtual community the problem can’t be related to harassment. So, there’s something else going on, is it that SO is designed for male competitiveness, being the site designed exclusively by males -there were no women on the team AFAIK-?

Isn’t it the reason you want diversity on your teams to start with? To provide a different perspective on the world, that enables you to reach everyone.

In my opinion, that’s why women should be part of the creation process, don’t you think?

None the less, a large group of men are acting as if they already know what women need, and as patriarchy mandates, providing it, creating programs, making conferences and burning witches, but not a single soul has asked women what they think, want, or need.

For a change, I’ve put up an anonymous survey online with the purpose of understanding how women who are already in tech, feel, if you have a female coworker, friend or colleague please share it, we may even find some interesting insights if we start listening.

I’m guilespi at Twitter

Survey

Share the link above or take the survey here:

This week my brother resigned the job he had for quite a few years. There comes a time for all of us when we need new challenges, and moving is the only way to keep learning and growing.

Today he gave me to read his “farewell letter”, his goodbye to co-workers. Far from commonplaces and standard templates, it was a really heartfelt goodbye, and what struck a chord with me, it’s that it was a thank you letter.

Thank you to the ones who gave me the opportunity, thank you to the ones who helped me, thank you to the ones who have shared your time with me, and thank you to the ones who made me better.

And I kept thinking, not about being thankful, which is by the way a great thing, but about trusting people and making opportunities for others.

We’re now living in a mincer, a people eater, with a permanent desire to crash each other, fiercely competitive startups, hiring and poaching, making sure every single hire is at the top of her game, because failure is not an option, and hey, we need that extra million.

Don’t we?

What is it that we have at the end of the game?

At least for me, the “thanks you” I’ve had, have made more for me than any money I can make , knowing that you’ve helped someone be better, or trusted someone when no one else would do it , that will stay with you when money is long gone, and it will probably stay when you are gone too.

Hiring only the very best is a safe bet anyone can take, having the talent to see potential takes skill, and having the guts to make opportunities and trust people not only takes courage, but it’s the only human thing to do.

Next time you’re about to put a cog on the machine, think human, and take the risk.

Rewards are worth it.

I’m guilespi at Twitter

When a language is going through its maturity process, there’s always the need for sample code and applications to look at, design patterns, coding guidelines, best libraries, you name it, you usually get those looking at the source code of others.

That is what really builds community, having a common language, besides the language.

Clojure’s been going through this phenomenon for the last years, as you see in this question from 2008 and this question still being answered in 2012.

This year I made a real life full application in Clojure so I’ve spent some time deciding on many strategies, where to put which code, how to test, best libraries to use and what not.

So I decided to put the source code online, not only because I think it may help someone, but hopefully somebody will come up and help me improve what it’s done in one way or another, it’s certainly far from perfect.

In case you wonder, it’s an application for automatic call and sms dispatching.

Among other things, you’ll find inside:

• Web development using ring, compojure and hiccup.
• Client side almost entirely done in clojurescript.
• Authentication and authorization using friend.
• Database access using both jdbc and korma.
• Async jobs using quartz for call and sms dispatching.
• Unit tests using midje.
• Chart drawing using incanter.
• Asterisk telephony integration using my own clj-asterisk bindings.
• Deploy configuration using pallet (not yet finished).

If you like it say hi! I’m guilespi